April 22 2014

PHP Benelux 2014

Solving the puzzle at PHPBenelux 2014

Last conference at the Dutch PHP Conference (DPC) I wrote a summary (in Dutch). This time I couldn't find the time, I took notes though, but I was/am too lazy. For PHP Benelux 2014 experiences you can read on other people their blogs, for example the one David wrote at his blog. And if you're looking for sheets, chances are you can find them at the event's joind.in page.

I made one big mistake at PHPBenelux, that was missing (by accident (don't ask why :p)) Ross Tuck's talk. Was really curious about that one. Of the other talks I especially liked Bastian Hofmann's talk "Marrying front with back end". His talk at DPC was also very good IIRC.

Dutch web alliance puzzle

An old collegue of mine (Marijn) and I decided to programmatically solve the puzzle created for the event there DWA. You can find the puzzle instructions in the photo I took (see fig.2.) We heard a rumour that you could win an ipad if you solved it. Unfortunately that wasn't true . In short you have to place all cubes side-by-side in such a way that rotating them combined should yield four unique labels each rotation step. There is only one possible solution.

We decided both on different approaches and see who would solve it first. Challenge accepted! I lost unfortunately, I even had to abandon my first approach and made the switch to semi-brute-force as soon as I gained more insight in how it could be solved more easily this way. Marijn approached it brute force from the start.

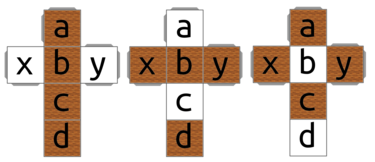
I gave each cube a number {1, 2, 3, 4}, and each sidename a letter {a, b, c, d, x, y}. Next I defined for each cube three directions {a, b, c, d}, {x, b, y, d} and {x, c, y, a} (see fig.1.). All these directions can also be in reverse ({d, c, b, a}, ...).

fig.1. possible directionsfig.2. puzzle instructions

My first idea was to place a cube on a side randomly, choosing for each cube a random direction to rotate in, and try four rotation steps. If in all steps the pictures were unique that would be a solution. I made a mistake in the implementation, totally forgot that {x, c, y, a} is also a possible sequence. What also didn't help is that I misread the instructions at first, thinking all sides had to be equal (instead of not-equal), which isn't possible if you take a good look at the actual cubes. I guess beer + coding isn't always a good combination.

My second approach was simply, generate "layouts" for each cube's three directions, i.e. for {a, b, c, d}:

{a, b, c, d}
{b, c, d, a}
{c, d, a, b}
{d, a, b, c}
{d, c, b, a}
{c, b, a, d}
{b, a, d, c}
{a, d, c, d}

For each cube a, b, c, d mean different side types (the different logos, php, phpbenelux, dwa, phpelephant). I simply compare every combination, and filter out the duplicate results. You initially get eight solutions, because every solution you can start at the first, second, third or fourth "step" of the solution, and eight because of the extra "times two" multiplier you get for forward versus backward rotation.

Solver in C++

Code also available on http://ideone.com/ttFYMD.

#include <iostream>
#include <algorithm>
#include <stdexcept>
#include <string>
#include <sstream>
#include <vector>
#include <array>
#include <iomanip>

enum class sidename
{
    a, b, c, d, x, y
};

enum class sidetype
{
    phpbenelux, php, phpelephant, dwa
};

std::string sidename_str(sidename sn) {
    switch (sn) {
        case sidename::a: return "a";
        case sidename::b: return "b";
        case sidename::c: return "c";
        case sidename::d: return "d";
        case sidename::x: return "x";
        case sidename::y: return "y";
    }
    throw std::runtime_error{"invalid sidename"};
}

std::string sidetype_str(sidetype st) {
    switch (st) {
        case sidetype::phpbenelux: return "phpbenelux";
        case sidetype::php: return "php";
        case sidetype::phpelephant: return "phpelephant";
        case sidetype::dwa: return "dwa";
    }
    throw std::runtime_error{"invalid sidetype"};
}

/**
 * cubes define 6 side types (or pictures)
 *
 * cubes calculate for themselves all possible layouts, meaning
 * if you rotate them into some direction, you get a side, followed by side+1, side+2, side+3.
 * there are a few possibilities: reverse order, and in each layout (or "path") you can start
 * rotating the cube on side, side+1, side+2 or side+4 (starting point "shifts").
 */
class cube
{
public:

    cube(sidetype a, sidetype b, sidetype c, sidetype d, sidetype x, sidetype y)
        : a_{a}, b_{b}, c_{c}, d_{d}, x_{x}, y_{y},
          directionnames_({{ 
             {sidename::a, sidename::b, sidename::c, sidename::d},
             {sidename::x, sidename::b, sidename::y, sidename::d},
             {sidename::a, sidename::y, sidename::c, sidename::x} }}),
          directions_({{ {a, b, c, d}, {x, b, y, d}, {a, y, c, x} }})
    {
        for (int i=0; i<4; i++) {
            for (auto &sides : directions_) {
                // normal insert
                layouts_.push_back(sides);

                // reverse insert
                auto sidesrev = sides;
                std::reverse(std::begin(sidesrev), std::end(sidesrev));
                layouts_.push_back(sidesrev);

                // shift all
                sidetype temp = sides[0];
                for (int i=1; i<=3; i++)
                    sides[i - 1] = sides[i];
                sides[3] = temp;
            }
        }
    }

    const std::vector<std::array<sidetype, 4>> & layouts() { return layouts_; }

private:

/**
 * This is how I labeled each sidetype:
 * 
 *    X  =   a
 *  X X X   = x b y 
 *    X  =   c
 *    X  =   d
*/

    sidetype a_;
    sidetype b_;
    sidetype c_;
    sidetype d_;
    sidetype x_;
    sidetype y_;

    std::array<std::array<sidename, 4>, 3> directionnames_;
    std::array<std::array<sidetype, 4>, 3> directions_;
    std::vector<std::array<sidetype, 4>> layouts_;
};

/**
 * helper class that can see if a given solution is a duplicate from a previous solution
 * 
 * if you have a solution that is simply the same one, but rotating in a different direction
 * is not really a new solution. also note the four possible starting point in each layout/path.
 * so it will check if duplicates exist in both forward and backward directions, and for each
 * possible four shifts
 */
class solutions
{
public:
    solutions()
    {}

    bool is_dupe(std::array<std::array<sidetype, 4>, 4> temp2)
    {
        // Check if found solution isn't a duplicate
        bool duplicate = false;
        for (auto &solution : solutions_) {
            for (int j=0; j<8; j++) {
                duplicate = true;
                int sidenum = 0;
                for (auto &side : solution) {
                    auto &temp = temp2[sidenum++];

                    int count = 0;
                    int offset = j % 4;
                    if (j < 4) {
                        // Check if they are duplicates, as we use offsets of +0, +1, +2, +3 we can 
                        //  detect shifted duplicate results.
                        for (auto i = side.begin(); i != side.end(); i++) {
                            duplicate = duplicate && temp[(count + offset) % 4] == *i;
                            count++;
                        }
                    }
                    else {
                        // Check if they are duplicates simply in reverse order, also with the 
                        //  detect for shifted duplicates.
                        for (auto i = side.rbegin(); i != side.rend(); i++) {
                            duplicate = duplicate && temp[(count + offset) % 4] == *i;
                            count++;
                        }
                    }
                }
                if (duplicate)
                       return true;
            }
        }

        // Remember found solution, for duplicates checking
        solutions_.push_back(temp2);

        return false;
    }

private:
    std::vector<std::array<std::array<sidetype, 4>, 4>> solutions_;
};

int main (int argc, char *argv[]) 
{
/*
 * on the sheet:
 * 
 *    cube 4 (sideways)
 * 
 *   cube 1, 2, 3
*/

    cube one{
        sidetype::dwa,
        sidetype::phpelephant,
        sidetype::phpbenelux,
        sidetype::dwa,
        sidetype::php,
        sidetype::phpbenelux};

    cube two{
        sidetype::phpelephant,
        sidetype::phpbenelux,
        sidetype::phpbenelux,
        sidetype::phpbenelux,
        sidetype::php,
        sidetype::dwa};

    cube three{
        sidetype::phpbenelux,
        sidetype::dwa,
        sidetype::phpelephant,
        sidetype::php,
        sidetype::dwa,
        sidetype::phpelephant};

    cube four{
        sidetype::php,
        sidetype::phpelephant,
        sidetype::phpbenelux,
        sidetype::phpelephant,
        sidetype::dwa,
        sidetype::php};

    solutions solution;

    for (auto &cube1sides : one.layouts()) {
    for (auto &cube2sides : two.layouts()) {
    for (auto &cube3sides : three.layouts()) {
    for (auto &cube4sides : four.layouts()) {

        // Pictures have to be unique on each four cubes to be considered a unique solution..
        bool flag = false;
        for (int i=0; i<4; i++) {
            // .. Also on each four rotations of course
            flag = flag || (!(cube1sides[i] != cube2sides[i] &&
                              cube1sides[i] != cube3sides[i] &&
                              cube1sides[i] != cube4sides[i] &&
                              cube2sides[i] != cube3sides[i] &&
                              cube2sides[i] != cube4sides[i] &&
                              cube3sides[i] != cube4sides[i]));
        }
        if (!flag){
            // Skip duplicate solutions
            if (solution.is_dupe({cube1sides, cube2sides, cube3sides, cube4sides})) {
                continue;
            }

            // Print the result
            std::cout << "The cube-layout for the solution:" << std::endl << std::endl;

            static auto print = [](const std::string &cube, decltype(cube1sides) &sides) {
                std::cout << cube << ": " 
                    << " front: " << std::setw(15) << sidetype_str(sides[0]) << ", "
                    << " up: " << std::setw(15) << sidetype_str(sides[1]) << ", "
                    << " top:   " << std::setw(15) << sidetype_str(sides[2]) << ", "
                    << " back:  " << std::setw(15) << sidetype_str(sides[3])
                    << std::endl;
            };

            print("cube #1", cube1sides);
            print("cube #2", cube2sides);
            print("cube #3", cube3sides);
            print("cube #4", cube4sides);
        }
    }}}}
}

Output:

cube #1:    front:             php,     up:     phpelephant,    top:        phpbenelux,     back:              dwa
cube #2:    front:      phpbenelux,     up:             dwa,    top:       phpelephant,     back:              php
cube #3:    front:     phpelephant,     up:      phpbenelux,    top:               dwa,     back:      phpelephant
cube #4:    front:             dwa,     up:             php,    top:               php,     back:       phpbenelux

Performance is on my pc 0,00202 seconds on average per run (see perf.txt). The average is 0,00181 seconds, 11.60% faster, if we stop processing when we find the 'first' solution.

I still think my first idea should also work and I'm curious if that "random brute-force" algorithm would on average find a solution faster compared to finding the first solution in my current solver (in terms of required compares). .